Mesolabium
|
1 Gerätedaten
Hersteller*.......: EratosthenesOrt, Land.........: Griechenland
Maße (LxBxH)......: unbekannt
Eingabe mit.......: Finger
System............: Analogrechner
Produziert........: ca. 240 v.Chr.
Produktionsmenge..: mindestens ein Stück
2 Beschreibung
Antikes Gerät zum Ziehen von Kubikwurzeln.
2.1 Die Geschichte
Die Legende berichtet, dass die Bewohner von Delos von einer Pestepidemie heimgesucht wurden. Das darob um Rat befragte Orakel von Delphi forderte sie auf, das Volumen des würfelförmigen Altars im Tempel des Apollon zu verdoppeln.Die mathematische Herausforderung dabei war, die Seitenlänge eines Würfels von doppeltem Volumen, bzw. die Zahl \sqrt[3]{2} zu konstruieren.
Dass das unter ausschließlicher Verwendung von Zirkel und Lineal nicht möglich ist, wurde erst im 19. Jahrhundert gezeigt, aber schon in der Antike wurden etliche Hilfskonstruktionen und Geräte entwickelt, die eine geometrische Konstruktion ermöglichten.
Das Mesolabium (oder Mesolab) stammt von Eratosthenes von Kyrene (276 - 194), der von seinem Mechanismus derart begeistert war, dass er ein Exemplar davon nebst Gebrauchsanweisung in einem Tempel als Weihegeschenk aufhängen ließ.
2.2 Das Gerät
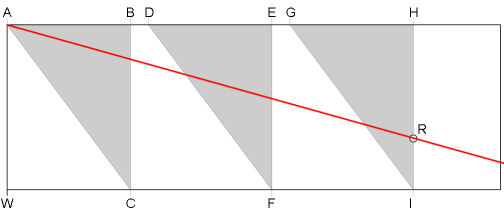
Das Mesolabium besteht aus einem Rahmen mit drei dreieckigen Tafeln ABC, DEF und GHI.
Die erste Tafel ABC ist fest montiert, die beiden anderen sind frei nach links und rechts verschiebbar.
Außerdem wird noch ein Lineal oder ein Faden (in der Abbildung rot) als Ablesehilfe benötigt.
2.3 Die Bedienung
Wie setzen im Folgenden die Länge der Strecke WA = 1 und nehmen an, dass die Zahl a, aus der die dritte Wurzel gezogen werden soll, kleiner als 1 ist (ist sie es nicht, so ersetzen wie sie durch ihren Kehrwert).
- Wähle den Punkt R auf der Strecke HI so, dass die Länge der Strecke IR = a, also gleich dem Radikanden ist.
- Mit P und Q bezeichne den jeweiligen Schnittpunkt der Hypotenuse des einen Dreiecks mit der senkrechten Kante des Dreiecks links von ihm.
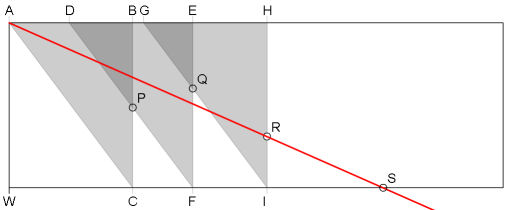
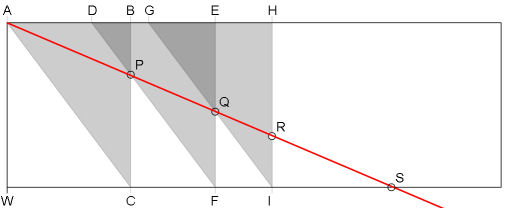
- Verschiebe die Dreiecke DEF und GHI so, dass A, P, Q und R auf einer Geraden liegen.
- Dann ist die Länge der Strecke CP gleich der gesuchten Kubikwurzel.
2.4 Die Mathematik
Um zu zeigen, warum das so ist, muss man ein bisschen mit ähnlichen Dreiecken jonglieren.
- Dreieck QFS: \frac{RI}{QF} = \frac{SI}{SF}
- Dreieck SFP: \frac{SI}{SF} = \frac{SQ}{SP}
- Dreieck SCP: \frac{SQ}{SP} = \frac{QF}{CP}
- Daraus folgt: \frac{RI}{QF} = \frac{QF}{CP}
- Also: (RI)*(CP) = (QF)^2
- Analog erhält man: \frac{QF}{CP} = \frac{CP}{1}
- Daraus bekommt man: QF =(CP)^2
- Also: (QF)^2 =(CP)^4 = (RI) * (CP)
- Und zuguterletzt : (CP)^3 = (RI).
Seite eröffnet von: Barbara 20:55, 14. Mai 2006 (IST)
Diese Seite darf an allen Stellen ergänzt werden,
die noch leer sind. Außerdem dürfen Zeilen hinzu gefügt werden.
Falls Sie mit einem bestehenden Inhalt nicht einverstanden sind,
machen Sie bitte einen Eintrag bei der Diskussion und schicken dem Ersteller der Seite eine Mail.
![[Hauptseite]](/upload/wiki.png)
 Hauptseite
Hauptseite