Wagner Planimeter

Inhaltsverzeichnis 1 Gerätedaten 2 Beschreibung 2.1 Bestandteile 2.2 Bedienung 2.3 Funktionsweise 3 Siehe auch 4 Literatur 5 Weblinks

1 Gerätedaten

Ort, Land.........: Deutschland
Maße (LxB) .......: 21 cm x 12 cm (Großer Winkel)
Maße (LxB) .......: 16,3 cm x 5 cm (Metalldreieck)
Maße (L) .........: 23,2 cm (grauer Stahlstab)
Gewicht...........: g
Eingabe ..........: manuell
System............: Planimeter, Proportionalrechner, Nichtintegrierendes Planimeter, Dreiecksplanimeter
Material..........: Messing, Stahl, Elfenbein (?)
Produziert........: (Beschreibung von 1821)

2 Beschreibung

2.1 Bestandteile

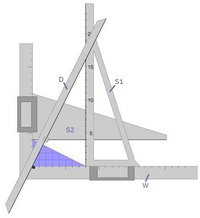
• Auf zwei orthogonal verbundenen Messingschienen läuft je ein dreieckiger Schieber, von denen der eine aus Metall, der andere aus Elfenbein oder einem ähnlichen Material ist.
• Am Elfenbeinschieber ist in 2,3 cm Abstand von der Laufschiene an einem Drehpunkt ein weiterer Stab befestigt.
• In den Metallschieber graviert ist eine lineare Skala deren Bereich von Null bis 160 reicht, dafür aber nur 151,4 mm in Anspruch nimmt. Außer dieser einen hat das Gerät keine weitere Skala. Außerdem findet sich auf diesem Schieber der Schriftzug "Für den Maßstab 1:1250"
• Zum Gerät gehört ein mit schwarzem Papier bezogenes Holzkästchen, das innen mit grünem Samt ausgekleidet ist.

2.2 Bedienung

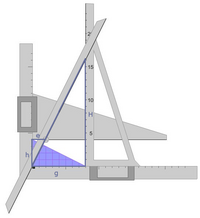
Das Gerät dient zur Messung geradlinig begrenzter Flächen auf Landkarten eines gegebenen Maßstabes (hier 1:1250). Dazu wird die zu vermessende Fläche zunächst in Dreiecke aufgeteilt, die einzeln wie folgt vermessen werden:

• Lege die Unterkante des Winkels W an die Grundseite des zu vermessenden Dreiecks, derart, dass die linke Ecke der Grundseite an die innere Ecke des Winkels anstößt.
• Schiebe den Schieber S1 an die rechte Ecke der Grundseite, und stelle mit dem Schieber S2 die Höhe des Dreiecks ein.
• Drehe den auf S2 montierten Dreharm D so, dass er den Anschlagpunkt in der Ecke des Winkels W berührt.
• Dann ist am Schnittpunkt von D mit S1 die Fläche abzulesen.

2.3 Funktionsweise

Das Wagnerplanimeter ist ein Proportionalrechner, der mit ähnlichen Dreiecken operiert.

Wenn das Planimeter wie oben beschrieben an das zu vermessende Dreieck mit der Grundseite g und der Höhe h angelegt ist, dann entsteht eine Figur mit zwei winkelgleichen rechtwinkligen Dreiecken: dem Dreieck mit den Katheten h und e und dem Dreieck mit den Katheten H und g.

Ähnlichkeitsbetrachtungen liefern uns \frac{H}{g} = \frac{h}{e} und damit H = \frac{1}{e} g h

Ist nun e so gewählt, dass es zwei Längeneinheiten im gegebenen Maßstab entspricht, so ist H = \frac{1}{2} g h , und damit gleich der Dreiecksfläche.

3 Siehe auch

•  noch eine Animation
• Cashmores Proportion Calculator
• Pediometer Schiereck

4 Literatur

• Hunäus 1864

5 Weblinks

•  http://ajmdeman.awardspace.info/1821wag.html Beschreibung des Geräts durch seinen Erfinder Professor G. Wagner

Seite eröffnet von: Barbara Haeberlin 20:32, 20. Mär 2007 (GMT)

Diese Seite darf an allen Stellen ergänzt werden, die noch leer sind. Außerdem dürfen Zeilen hinzu gefügt werden.
Falls Sie mit einem bestehenden Inhalt nicht einverstanden sind, machen Sie bitte einen Eintrag bei der Diskussion und schicken dem Ersteller der Seite eine Mail.

Bearbeiten | Artikeldiskussion | Versionen | Artikel, die hierhin verweisen | Verlinkte Seiten Diese Seite wurde bisher 15498 mal abgerufen. Diese Seite wurde zuletzt geändert um 12:32, 28. Apr 2023.