Speichervorrichtungen bei mechanischen Vierspezies-Rechenmaschinen
von Harald Schmid, Amberg
|
1 Vorwort
Die Möglichkeit, Zahlen und Ergebnisse für die Weiterverarbeitung in einem Speicher abzulegen, war eine wesentliche Voraussetzung für die Entwicklung des Computers. Heutzutage verwendet man Transistoren zu diesem Zweck, während Konrad Zuse bei den ersten programmierbaren Rechenanlagen, der Z1 von 1941 und der Z3 aus dem Jahr 1944, noch mechanische Elemente (verschiebbare Metallplättchen) bzw. elektromechanische Bausteine (Relais) benutzt hat. Der Computerspeicher hat seine Wurzeln also in der Mechanik. Speichervorrichtungen findet man jedoch nicht nur im Computer, sondern auch bei "einfachen" Rechenmaschinen ohne programmgesteuerten Rechenablauf. So hat fast jeder moderne elektronische Tisch- und Taschenrechner die Tasten M+ und M-, mit welchen man einen Wert aus dem Anzeigewerk in einem Speicher ablegen oder additiv bzw. subtraktiv zu dessen Inhalt hinzufügen kann. Durch Betätigung der Taste MR läßt sich dann der abgespeicherte Wert jederzeit wieder in den Rechenablauf einbringen. Der wesentliche Vorteil eines solchen Speichers ist, daß man Zwischenergebnisse nicht per Hand niederschreiben und erneut eintasten muß, so daß auch umfangreiche Rechenaufgaben ohne Unterbrechung und Eingabefehler ausgeführt werden können. Verschiedene Arten der Speicherung gab es auch schon bei den Vorgängern der Tischrechner, den mechanischen und elektrisch-mechanischen Vierspezies-Rechenmaschinen. Bei der Werteverarbeitung und in der technischen Umsetzung findet man allerdings große Unterschiede. Da solche Speicherwerke in der Literatur meist nur als Zusatzeinrichtung am Rande behandelt werden und detaillierte Informationen in Katalogen (z.B. dem Büromaschinenlexikon) fehlen, sollen im folgenden die einzelnen Speichertypen und -verfahren bei Vierspezies-Rechenmaschinen etwas ausführlicher vorgestellt werden.
2 Historische Entwicklung
2.1 Der Begriff "Speicherwerk"
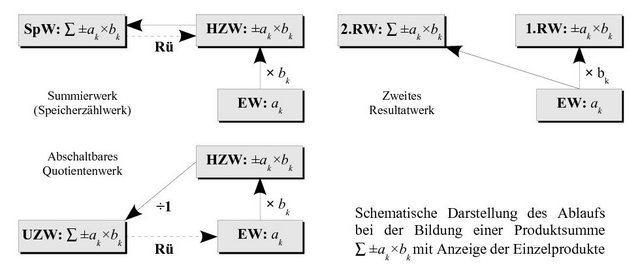
Früher hatte das Wort "Speichern" in der Rechentechnik eine andere Bedeutung als heute. Bei einem Computer ist der Speicher ein Medium (z.B. Arbeitsspeicher oder Datenträger), in dem beliebige Nutzdaten abgelegt und zu einem späteren Zeitpunkt wieder abgerufen werden können. Im Zusammenhang mit Rechenmaschinen war das Speicherwerk ursprünglich nur eine ergänzende Einrichtung, um bei der Summierung von Produkten, die im Hauptzählwerk automatisch erfolgt, auch die Einzelprodukte ablesen zu können (vgl. Willers [3], Abschnitt I.C.2.i). Genau diese Anforderungen erfüllen das Summierwerk und ein zweites Resultatwerk: Die Produkte werden im Hauptzählwerk gebildet und nachträglich (Summierwerk) oder gleichzeitig (zweites Resultatwerk) im Speicherwerk gesammelt - man spricht daher auch von akkumulativen Speichervorrichtungen. Eine ähnliche Funktion hat das zweite Umdrehungszählwerk, in dem sich Quotienten aufsummieren lassen, wobei die Einzelquotienten im ersten Umdrehungszählwerk abgelesen werden können. Die genannten Vorrichtungen erlauben eingeschränkt auch eine Weiterverarbeitung der gespeicherten Werte. Bei vielen Modellen kann der Inhalt des Summierwerks wieder in das Resultatwerk übertragen werden, so daß er beispielsweise als Dividend zur Verfügung steht, und bei den meisten Duplexmaschinen ist eine Division auch direkt aus dem zweiten Hauptzählwerk möglich. Näher am modernen Speicherbegriff sind die Einrichtungen der Brunsviga 20 (gesplittetes Resultatwerk) oder der Rheinmetall KEL IIc RS (Rückwurfspeicher). Bei diesen Vierspeziesmaschinen kann der Inhalt des Speichers wieder in das Einstellwerk gebracht und somit auch als Summand, Multiplikand oder Divisor weiterverarbeitet werden. Speicher im heutigen Sinn findet man allerdings erst bei den mechanischen Rechenmaschinen der letzten Generation, den druckenden Rechenautomaten wie etwa der Diehl Transmatic S oder dem Modell 166 von Precisa. Diese Maschinen arbeiten mit Zahnstangen, um einen Wert aus dem Einstell-, Rechen- oder Speicherwerk "abzufühlen" und an ein anderes Zählwerk bzw. das Druckwerk weiterzugeben alle beteiligten Zählwerke werden hierzu in geeigneter Weise mit den Zahnstangen gekoppelt. Auf diese Weise ist ein beliebiger Werteaustausch zwischen Rechen- und Speicherwerken möglich.
2.2 Technische Entwicklung
Die Geschichte der Vierspezies-Rechenmaschinen geht bekanntlich zurück auf Gottfried Wilhelm Leibniz, der bereits 1671 die erste Rechenmaschine mit Staffelwalzenantrieb konstruierte (und wohl auch der Erfinder des Sprossenradsystems ist). Bis zur Mitte des 19. Jahrhunderts wurden Vierspeziesmaschinen hauptsächlich als Einzelstücke hergestellt, und die technische Herausforderung lag in der Entwicklung einer zuverlässigen Mechanik. Erst die Massenproduktion, die ab 1820 in Frankreich (Arithmomètres von C. X. Thomas) und etwas später in Deutschland (1878, Arthur Burkhardt, Glashütte/Sachsen) einsetzte, machte Vierspezies-Rechenmaschinen für den alltäglichen Einsatz in Büros interessant. Damit stiegen auch die Anforderungen an solche Maschinen. Spezielle Aufgabenstellungen aus dem kaufmännischen Bereich, z.B. Fakturierungen und Lohnrechnungen, oder besondere Rechenprobleme aus den Ingenieur- und Naturwissenschaften (Vermessungswesen, Statistik und Astronomie, vgl. Veithen [1]) brachten die Konstrukteure Anfang des 20. Jahrhunderts dazu, über Speichermöglichkeiten in Vierspezies-Rechenmaschinen nachzudenken. Der wohl erste Entwurf zum Einbau einer zusätzlichen Speichereinrichtung in eine Vierspeziesmaschine geht zurück auf den Ingenieur Franz Trinks, der auch die Braunschweiger Nähmaschinenfabrik Grimme, Natalis & Co. zum bedeutensten Hersteller von Sprossenradmaschinen machte. Seine 1901 ausgegebene Patentschrift DE125471 mit dem Titel "Vorrichtung an Rechenmaschinen zur Sichtbarmachung der Einzelsummanden bei fortgesetzter Addirung von Produkten" beschreibt eine Sprossenrad-Rechenmaschine, bei der ein Wert aus dem Einstellwerk gleichzeitig in zwei Anzeigewerke übertragen wird. Mit diesem Patent hat Franz Trinks die Grundlagen für das Parallelwerk gelegt. Seine Konstruktion wurde jedoch erst 1908 im Modell Brunsviga G umgesetzt. Im gleichen Jahr hat Ernst Schuster (bzw. Chr. Hamann, siehe Reese [10]) eine Sprossenradmaschine mit Summierwerk, also mit einem vom Hauptzählwerk unabhängigen Speicherzählwerk zur Aufsummierung von Produkten, vorgestellt. In der Patentschrift DE143497 "Rechenmaschine zur Summierung von Produkten mit getrennten Anzeigewerken für die Einzelprodukte und deren Summe" vergleicht Schuster seine Konstruktion mit dem Vorschlag von Trinks:
- "Es ist auch bereits eine Vorrichtung bekannt, welche den gleichen Zweck verfolgt wie die vorliegende Maschine und auch zwei Anzeigewerke mit einem gemeinsamen Zählwerk besitzt. Diese Vorrichtung ist so eingerichtet, daß die die Endresultate aufnehmenden Räder abermals Räder zur Anzeigung der Produkte bewegen, die während jeder Umdrehung des Zählwerkes, nach Beendigung der Wertübertragung, aber vor erfolgter Zehnerschaltung, außer Eingriff mit den sie antreibenden Rädern gebracht werden. Hier werden also die beiden Anzeigewerke zu gleicher Zeit, durch Vermittlung des Anzeigewerkes für die Summe auch das Anzeigewerk für die einzelnen Produkte, von dem Zählrad beeinflußt. Das gleichzeitige Antreiben der Anzeigewerke ist aber aus praktischen Gründen nicht angängig, weil die Maschine dadurch einen doppelt so schweren Gang bekommt und doppelt so viel Geräusch verursacht. Auch müssen bei genannter Einrichtung vor Beginn einer Zehnerschaltung, welche bei jeder Kurbeldrehung erfolgen kann, die Anzeigewerke voneinander entfernt werden, um nach erfolgter Zehnerschaltung wieder miteinander in Eingriff zu kommen. Da nun das Anzeigewerk für die einzelnen Produkte mit all seinen Teilen ein Gewicht von etlichen Kilogramm hat und bei jeder Kurbeldrehung, welche bei mäßig raschem Rechnen zweimal in der Sekunde erfolgen kann, hin- und herpendelt, so ist wohl erklärlich, daß die Erschütterungen und das Geräusch störend werden und die in Anspruch genommenen Teile einer größeren Abnutzung unterworfen sind. Um daher den Gang der aus der Patentschrift 7393 bekannten Maschine (Sprossenradmaschine nach Odhner, Anm. des Autors) durch Hinzufügung des zweiten Anzeigewerkes nicht zu beeinträchtigen, ist die Einrichtung getroffen, daß nur ein Anzeigewerk c von dem Zählrad a eingestellt wird, und daß während der ganzen Dauer der Bildung eines Produktes die beiden Anzeigewerke c und f außer Eingriff stehen, und ein solcher nur dann zu erfolgen braucht, wenn das in dem Anzeigewerk c gebildete Produkt zum Zwecke einer Summierung auf das andere Anzeigewerk übertragen werden soll."
Ernst Schuster hat auch zusätzliche Einrichtungen für das Summierwerk entwickelt, wie z.B. die Zehnerübertragung (Patentschrift DE163937) und den Postenzähler (Patent DE163938). In seiner Berliner Fabrik wurden aber nur wenige Sprossenradmaschinen "Berolina Duplicator" mit Summiervorrichtung hergestellt (siehe Reese [10], S. 53ff). Stattdessen hat Schuster ein späteres Modell, gebaut um 1923, mit einem Parallelwerk ausgestattet. Die erste kommerzielle Vierspezies-Rechenmaschine mit Parallelwerk wurde 1907 in der Rechenmaschinenfabrik von Ludwig Spitz hergestellt: das Modell TIM mit Doppellineal. Diese Staffelwalzenmaschine, entwickelt von Robert Rein, wurde später unter dem Namen "Unitas" verkauft und ist in der Patentschrift DE216561 von 1906 beschrieben. Die wesentliche Neuerung bei dieser Konstruktion war der Einbau eines zweiten Hauptzählwerks, das abgeschaltet und unabhängig vom ersten gelöscht werden konnte. Eine weitere Duplexmaschine, das Austria-Zwillingsmodell, hat Samuel Herzstark 1908 auf den Markt gebracht. Während bei der TIM Unitas beide Zählwerke von einer Staffelwalzenreihe angetrieben werden, haben die zwei Hauptzählwerke dieser "Zwillings-Thomas-Maschine" (vgl. Patent DE221819) jeweils einen eigenen Staffelwalzenantrieb. Ein derartiger Mechanismus wurde allerdings schon 1906 von Hugo Wurfschmidt in seiner Patentschrift DE210660 vorgeschlagen. In den nachfolgenden Jahren haben dann auch weitere namhaften Rechenmaschinen-Hersteller Patente für den Einbau eines zweiten Anzeigewerks angemeldet, wie z.B. Archimedes (Reinhold Pöthig, AT61296, 1909) und Badenia (Mathias Bäuerle, DE221284 bzw. DE348426, 1909/13). Die erste Rechenmaschine mit einem zweiten Umdrehungszählwerk, das auch zum Abspeichern und Aufsummieren von Quotienten verwendet werden kann, war das Modell H von Brunsviga, gebaut von 1908 bis 1913. Diese Maschine wurde nach dem Patent CH45660 von Franz Trinks entwickelt, der auch die Grundlage für einen weiteren Speichermechanismus legte: das geteilte Resultatwerk. Die bisher erwähnten Speicherwerke haben gemeinsam, daß zum Abspeichern von Produkt- oder Quotientensummen ein zusätzliches Zählwerk in die Maschine eingebaut werden muß. Beim gesplitteten Resultatwerk verzichtet man auf einen Teil des Hauptzählwerks, um ihn für die Produktsummierung zu nutzen. Die erste kommerzielle Vierspezies-Rechenmaschine mit einer solchen Speichervorrichtung war jedoch erst das Modell Brunsviga Nova IVa, das ab 1925 gebaut und 1934 vom Modell Brunsviga 20 abgelöst wurde. Das Konzept hierzu findet man allerdings schon in den Patentschriften AT54949 bzw. CH58240 von Franz Trinks aus dem Jahr 1911.
Ab etwa 1912 wurden viele Vierspezies-Rechenmaschinen der gehobenen Preisklasse mit einem Speicherwerk ausgestattet. Die erste Maschine nach dem Proportionalhebel-Prinzip mit Speicherwerk war die Mercedes Euklid 5, entwickelt um 1913 von Christel Hamann (vgl. Patent DE278680). In dieses und in weitere Mercedes Euklid-Maschinen bis zum Modell Cellatron R 44 SM, das noch 1969 hergestellt wurde, hat man ein Summierwerk eingebaut. Ein solches findet man auch in der ersten elektrifizierten Sprossenradmaschine L'Eclair/Sanders, produziert von 1912 bis 1929 nach den Patenten DE274744 von Roberto Piscicelli bzw. DE420470 von Nico Sanders, sowie in den vollautomatischen Rechenmaschinen Hamann Selecta SP mit Schaltklinkenantrieb, hergestellt von 1931 bis ca. 1940, oder in der Staffelwalzenmaschine Rheinmetall SASL ("Super-Automat mit Speicher und elektrischer Löschvorrichtung"), das 1932 auf den Markt kam und später unter der Bezeichnung SARS noch bis 1964 produziert wurde. Besonders vielfältige Speichermöglichkeiten boten etwa die vollautomatischen Rechenmaschinen MADAS 20 ATG (später 20 BTG), gebaut von 1936 bis 1967, sowie "Speicherautomaten" der 1960er Jahre, wie etwa das Monroe-Modelle 88N-213, die u.a. über zwei Haupt- und Umdrehungszählwerke verfügen. Der Schweizer Madas-Hersteller Hans W. Egli war es auch, der 1936 Staffelwalzenmaschinen mit einem völlig andersartigen Speichermechanismus präsentierte: die Handkurbelmaschine 10 R und das elektrische Modell 20 S. Diese Maschinen besitzen einen Mechanismus zur Rückübertragung in das Einstellwerk, der gleichzeitig auch zum Abspeichern der Werte aus dem Hauptzählwerk verwendet wird. Ein ähnliches Speicherverfahren war allerdings schon im Modell Kuhrt AB von 1923 vorhanden. Bei dieser Schwenksprossenradmaschine wird der Wert aus dem Resultatwerk durch Abfühlen der Ziffernrollen in einen Merkspeicher eingetragen und kann später in das Einstellwerk gebracht werden (vgl. hierzu Anthes [8] sowie den Eintrag  Kuhrt bei Landwehr [15]; zur Rückübertragung siehe auch die Patentschrift DE344259 von Ernst Kuhrt bzw. das Patent DE578683 der Brunsviga-Maschinenwerke, welche die Firma Kuhrt im Jahr 1927 übernahmen). Die mechanischen Rechenmaschinen aus der letzten Generation, druckende Vierspezies-Rechenautomaten wie z.B. die Diehl Transmatic S oder das Modell 600 von Hamann, waren dann schon mit Speicherwerken ausgestattet, welche jedes Zwischenergebnis, egal ob Summe, Produkt oder Quotient, sofort aufnehmen können, wobei sich der gespeicherten Wert auch jederzeit wieder in den laufenden Rechenvorgang einbringen läßt. Diese Art der Speicherung ist dann kaum mehr von den Speichermöglichkeiten elektronischer Tischrechenmaschinen zu unterscheiden, die ab ca. 1961 auf den Markt kamen und schon früh mit akkumulativen Speicherwerken bzw. Konstantenspeicher ausgeliefert wurden (z.B. IME 84 oder Sharp Compet CS10A aus dem Jahr 1964). Man findet diese Speichervorrichtungen auch heute noch auf jedem handelsüblichen Taschenrechner in Form der Tasten M+, M- und MR.
Kuhrt bei Landwehr [15]; zur Rückübertragung siehe auch die Patentschrift DE344259 von Ernst Kuhrt bzw. das Patent DE578683 der Brunsviga-Maschinenwerke, welche die Firma Kuhrt im Jahr 1927 übernahmen). Die mechanischen Rechenmaschinen aus der letzten Generation, druckende Vierspezies-Rechenautomaten wie z.B. die Diehl Transmatic S oder das Modell 600 von Hamann, waren dann schon mit Speicherwerken ausgestattet, welche jedes Zwischenergebnis, egal ob Summe, Produkt oder Quotient, sofort aufnehmen können, wobei sich der gespeicherten Wert auch jederzeit wieder in den laufenden Rechenvorgang einbringen läßt. Diese Art der Speicherung ist dann kaum mehr von den Speichermöglichkeiten elektronischer Tischrechenmaschinen zu unterscheiden, die ab ca. 1961 auf den Markt kamen und schon früh mit akkumulativen Speicherwerken bzw. Konstantenspeicher ausgeliefert wurden (z.B. IME 84 oder Sharp Compet CS10A aus dem Jahr 1964). Man findet diese Speichervorrichtungen auch heute noch auf jedem handelsüblichen Taschenrechner in Form der Tasten M+, M- und MR.
2.3 Wirtschaftliche Aspekte

Abb. 4: Einfache elektrische Staffelwalzenmaschine Rheinmetall KEW Ie S mit Summierwerk (aus einem Prospekt)
"Es sind sowohl Handmaschinen als Halbautomaten und Vollautomaten mit einem Summierwerk versehen. Da dasselbe nur für Multiplikationszwecke dient, hat man sogar bei motorisch angetriebenen Maschinen mit dieser Ausführung die Einrichtung der vollautomatischen Division fallen gelassen, um möglichst billige Summierwerkmaschinen schaffen zu können" (A. Schranz). Eine mit Speicherwerk ausgestattete Rechenmaschine ermöglicht sowohl die Überprüfung als auch die Weiterverarbeitung von Zwischenresultaten, aber das hatte seinen Preis. Die Maschine mußten mit einem weiteren Zählwerk und zusätzlichen Übertragungsvorrichtungen ausgestattet werden, was einen erheblichen Mehraufwand in der Konstruktion erforderte. Beispielsweise kostete 1958 die Rechenmaschine TEH 10 von Badenia rund 1000 DM, während das Modell TEH 10 Duplex mit Parallelwerk fast doppelt so teuer war, und für eine Diehl EvMS 15 mußte man immerhin 50% mehr bezahlen als für das Basismodell EvM 15 ohne Summierwerk. Ein weiteres Problem war die Störanfälligkeit. Speicherautomaten besitzen einen komplexen Aufbau, so daß bereits kleine Ungenauigkeiten in der Justierung oder eine falsche Bedienung durch den Anwender zu einer Blockierung der gesamten Mechanik führen können. Diese Modelle mußten daher häufiger repariert und gewartet werden, weshalb sie nicht selten sehr unbeliebt waren. Dies mag auch ein Grund dafür sein, warum zahlreiche Hersteller ihre Speichermaschinen schon bald wieder aus dem Programm nahmen. Bei nicht allen Modellen war die Konstruktion so ausgereift, daß sie auch über Jahrzehnte hinweg verkauft wurden, wie etwa die Brunsviga 20 (vgl. Metzen [11]).
3 Speichertechnik
Das Speicherwerk gehört nicht zur Grundausstattung einer Vierspeziesmaschine. Es zählt vielmehr zu den "besonderen Einrichtungen, die mehr oder weniger entbehrlich, wenn auch oft sehr nützlich sein können" (W. Meyer zur Capellen). Um den Nutzen eines Speicherwerks einordnen zu können, wird im folgenden zunächst die Funktionsweise einer Vierspeziesmaschine in Standardausführung skizziert und deren Fähigkeit zur Weiterverarbeitung von Ergebnissen beschrieben. Zuerst bringt man eine Zahl mittels Hebel oder Tasten in das Einstellwerk der Maschine. Bei jedem Umlauf der Antriebswelle wird dann der Wert im Einstellwerk zum Inhalt des Hauptzählwerks addiert oder davon subtrahiert, während das Umdrehungszählwerk die Anzahl der Umläufe registriert. Das Hauptzählwerk muß eine Vorrichtung zur selbsttätigen Zehnerübertragung besitzen. Das Umdrehungszählwerk sollte ebenfalls eine Zehnerübertragung haben und die Umläufe der Antriebswelle sowohl positiv als auch negativ zählen können. Die Übertragung eines Wertes vom Einstellwerk in das Hauptzählwerk sowie das Umschalten zwischen Addition und Subtraktion erfolgt durch das Schaltwerk. Zusätzlich besitzt die Vierspeziesmaschine einen beweglichen Schlitten, der entweder das Einstellwerk oder das Hauptzählwerk trägt und mit dem man auf andere Dezimalstellen übergehen kann. Das ist die Grundlage für die schnelle Multiplikation und Division, die man auf Additionen, Subtraktionen und geeignete Schlittenverschiebungen zurückführt. Das Hauptzählwerk, auch Produkt- oder Resultatwerk genannt, liefert dann das Ergebnis einer Multiplikation, während im Umdrehungszählwerk der Multiplikator angezeigt wird. Unterbleibt das Löschen des Hauptzählwerks zwischen einzelnen Multiplikationen, so werden dort automatisch Produktsummen der Form ∑ ±ak×bk = ±a1×b1 ± a2×b2 … gebildet. Ein Wert im Hauptzählwerk kann unmittelbar als Summand, Minuend oder Dividend weiterverarbeitet werden. Bei der Division wird der Divisor im Einstellwerk so oft vom Dividenden im Hauptzählwerk subtrahiert, bis dieses den Wert Null oder nur noch einen hinreichend kleinen Rest enthält. Der Quotient erscheint dann im Umdrehungszählwerk, falls dieses gegenläufig zur Antriebsvorrichtung arbeitet. Ebenso kann der Wert im Umdrehungszählwerk direkt als Multiplikator weiterverarbeitet werden, indem man den Multiplikanden im Einstellwerk so oft zum Inhalt des Hauptzählwerks addiert, bis der Wert im Umdrehungszählwerk auf Null zurückgedreht ist. Auf diesen Mechanismen beruhen auch die automatische Multiplikation und Division: Ein Operand im Zählwerk wird durch fortgesetztes Addieren oder Subtrahieren der zu verarbeitenden Zahl im Einstellwerk auf Null gebracht, wobei die Schlittenverschiebung und das Umschalten der Drehrichtung der Antriebswelle durch den Zehnerübertrag in der höchsten Stelle des Zählwerks gesteuert werden. Die meisten automatischen Vierspeziesmaschinen verfügen über ein eigenes Multiplikatorwerk, das statt des Umdrehungszählwerks den Multiplikator aufnimmt. Indem man durch Eins dividiert oder mit Eins multipliziert und den Drehsinn des Umdrehungszählwerks geeignet wählt, kann man einen Wert positiv oder negativ vom Hauptzählwerk in das Umdrehungszählwerk und umgekehrt übertragen. Verfügt die Maschine zusätzlich über eine Einrichtung zur Rückübertragung vom Hauptzählwerk in das Einstellwerk, so kann ein Rechenergebnis wiederum als Summand, Subtrahend, Multiplikand oder Divisor verarbeitet werden. Um durch eine Zahl aus dem Einstellwerk zu teilen, bildet man zunächst deren reziproken Wert im Umdrehungszählwerk, indem man den Wert im Einstellwerk zum Inhalt des Hauptzählwerks addiert, bis dort wieder Null erscheint (Division im Plussinn mit gedachter Außen-Eins). Anschließend multipliziert man das Ergebnis mit dem neu eingetasteten Dividenden im Einstellwerk. Bei einer Vierspeziesmaschine mit dieser Grundausstattung läßt sich demnach das Ergebnis im Hauptzählwerk ohne erneutes Eintasten mit einer Zahl aus dem Einstellwerk über alle vier Grundrechenarten in beliebiger Weise verarbeiten. Allerdings gibt es keine Möglichkeit, zwei Resultate (zusammengesetzte Ausdrücke) unabhängig voneinander zu berechnen, um sie später ohne Wiedereintasten miteinander zu verknüpfen. Selbst bei einer einfachen Produktsumme a×b + c×d können die Einzelprodukte nicht mehr getrennt angezeigt werden. Zu diesem Zweck gibt es das Speicherwerk eine Vorrichtung zum Aufbewahren berechneter Werte für die Weiterverarbeitung zu einem späteren Zeitpunkt. Eine mit Speicherwerk ausgestattete Vierspezies-Rechenmaschine eröffnet vielfältige Anwendungsmöglichkeiten. Insbesondere Verfahren aus der Numerischen Mathematik lassen sich mit Speichermaschinen besonders vorteilhaft durchführen. Als Beispiele seien hier nur die numerische Integration (z.B. Trapezformel und Simpson-Regel), die Auswertung von Polynomen nach dem Horner-Schema sowie das Lösen linearer Gleichungssysteme (siehe Willers [3], Abschnitt I.C.3.e) erwähnt. Speichervorrichtungen kann man einteilen in akkumulative Speicherwerke (Speicherzählwerke) mit eigener Zehnerübertragung und in nichtakkumulative Speicherwerke (Wert- oder Merkspeicher) ohne Zehnerübertragung, aber mit einer Rückwurfeinrichtung in eines der übrigen Zählwerke. Die mechanischen Elemente, die zur Speicherung einer Zahl verwendet werden, können sehr unterschiedlich sein. Man findet Speicherwerke, die mit Radsätzen, Zahnstangen, Stufenwalzen oder Abtastscheiben arbeiten. Außerdem kann das Speicherwerk entweder unsichtbar oder mit einem Anzeigewerk zur Kontrolle des gespeicherten Werts verbunden sein. Zwei extrem unterschiedlichen Ausführungsformen des Speicherwerks sind zum Beispiel:
- Das Summierwerk der Rheinmetall SASL: Diese Staffelwalzenmaschine hat ein sichtbares Speicherzählwerk im Schlitten. Der Wert im Speicher wird ähnlich wie beim Hauptzählwerk durch Drehen von Zahnrädern eingestellt und mittels Ziffernrollen angezeigt. Das Speicherwerk besitzt eine Zehnerschaltvorrichtung, und es verfügt sogar über ein eigenes Wendegetriebe, so daß man Werte addieren oder subtrahieren kann. Die Wertübertragung vom Resultatwerk in das Speicherwerk und umgekehrt erfolgt gleichzeitig mit dem Löschen der zu übertragenden Zahl.
- Das Multiplikatorwerk der Facit ESA: Hier wird gleichzeitig mit dem Eintasten ein Wert im unsichtbaren Multiplikatorspeicher abgelegt. Dieses besteht aus einzelnen Scheiben mit unterschiedlich tiefen Einschnitten, die um einen den Ziffern entsprechenden Winkel gedreht werden. Bei einer Multiplikation wird der gespeicherte Wert nur abgetastet, so daß er auch nach der Produktbildung im Speicherwerk erhalten bleibt (konstanter Multiplikator). Das Speicherwerk erfordert keine Zehnerübertragung, und es kann nur Werte über das Einstellwerk aufnehmen.
Im folgenden werden grundlegenden Merkmale der verschiedenen Speichervorrichtungen zusammengestellt. Bei den akkumulativen Speicherwerken ist die Werteverarbeitung für die "klassische Speicheraufgabe", die Bildung einer Produktsumme mit Anzeige der Einzelprodukte, beschrieben. Die nichtakkumulativen Speicher sind nach dem Übertragungsweg zwischen den beteiligten Werken geordnet. Bei den einzelnen Speicherverfahren sind jeweils auch einige typische Rechenmaschinen-Modelle mit ihren Besonderheiten aufgelistet und soweit bekannt die zugehörigen Patentschriften angegeben. Betrachtet werden hier nur elementare Speicherverfahren bei Vierspeziesmaschinen. Nicht berücksichtigt sind Doppel- und Dreifachmaschinen (z.B. Thales GEO/R oder Brunsviga 183) sowie Addier-, Buchungs- und Fakturiermaschinen, die ebenfalls über vielfältige Speichermöglichkeiten verfügen, wie z.B. die ab 1932 hergestellte Rheinmetall-Fakturiermaschine mit mehreren Speicherwerken und elektromechanischer Abfühlvorrichtung.
3.1 Akkumulative Speicherwerke
Summierwerk. Das Summierwerk, auch Übernahmespeicher oder Sammelwerk genannt, ist eine Vorrichtung zum Aufsummieren von Werten aus dem Resultatwerk, welche insbesondere die getrennte Anzeige von Einzelprodukten und deren Gesamtsumme ermöglicht. Man kann Summierwerke in zwei Gruppen einteilen: in Speicherzählwerke mit eigener Zehnerübertragung und in Wertspeicher ohne Zehnerübertragung, die jedoch bei der Aufsummierung von Zahlen mit dem Resultatwerk zusammenarbeiten. Die Wertübertragung in das Summierwerk erfolgt in beiden Fällen gleichzeitig mit dem Löschen der zu speichernden Zahl aus dem Resultatwerk. Hierbei wird jede Ziffer im Resultatwerk um den angezeigten Betrag zurückgedreht, und diese Drehung wird an die einzelnen Stellen im Speicherwerk weitergegeben. Ist die Rechenmaschine mit einem Speicherzählwerk ausgestattet, so kann man im Hauptzählwerk einzelne Produkte bilden und diese unmittelbar im Speicherzählwerk aufsummieren. Meist ist für die Wertübertragung in das Speicherzählwerk ein eigenes Wendegetriebe vorgesehen, so daß die Zahl im Hauptzählwerk auch vom gespeicherten Wert subtrahiert werden kann. Hat die Maschine dagegen einen Wertspeicher ohne Zehnerübertragung, dann sind für die getrennte Anzeige von Produktsumme und Einzelprodukten zwei Schritte nötig: Nachdem man ein Produkt berechnet hat, wird die bereits gespeicherte Produktsumme in das Resultatwerk übertragen und zu dessen Inhalt addiert (die Zehnerübertragung erfolgt also im Hauptzählwerk). Anschließend wird die neue Produktsumme wieder in das Speicherwerk gebracht. Einen solchen Wertspeicher mit Summiervorrichtung, der wesentlich einfacher aufgebaut ist als das Speicherzählwerk, findet man bei den Rechenmaschinen Mercedes Euklid. Der Inhalt des Speicherwerks kann hier allerdings nur additiv in das Resultatwerk übertragen werden. Daher muß man zur Berechnung einer Differenz den Komplementwert einer Zahl abspeichern. Bei der Mercedes Euklid ist hierfür ein Komplementwerk eingebaut, mit dem sich eine Zahl im Resultatwerk sofort positiv oder negativ verarbeiten läßt. Alle Modelle mit Summierwerk haben eine Vorrichtung zur Rückübertragung des gespeicherten Werts in das Hauptzählwerk, wobei die Übertragung durch Nullstellen des Speicherwerks erfolgt. Einige Maschinen besitzen außerdem noch einen Postenzähler, der die Anzahl der Speichervorgänge registriert. Da ein Summierwerk unabhängig vom verwendeten Antriebsmechanismus ist und eine eigene Übertragungsvorrichtung erfordert, findet man diese Speichervorrichtung bei Rechenmaschinen jeder Bauart. Es wurde vielfach als Zusatzeinrichtung bei einem vorhandenen Basismodell angeboten (gekennzeichnet durch ein "S" in der Modellbezeichnung). Einige dieser Maschinen hat man wahlweise auch mit einer Auf- und Abrundungsvorrichtung angeboten, wie z.B. die Modelle von Diehl oder Rheinmetall.
| Hersteller | Modelle | System | Besonderheiten | Patente |
|---|---|---|---|---|
| Diehl | EvMS 15/18, DSR 15/18, VSR 18 | Staffelwalze | Speicherzählwerk im Schlitten, Modelle A/A zusätzlich mit Auf- und Abrundungsvorrichtung, Produktsummierung automatisch oder mit Taste ⊕ | DE1144511 DE1124742 |
| Hamann | Selecta SP, Selecta SPU |
Schaltklinke | Stationäres Speicherzählwerk, wahlweise mit Auf- und Abrundungseinrichtung; Abspeichern mit Taste 00, Rückwurf in das Hauptzählwerk mit Kurbel; Postenzähler; Modell SPU mit zweitem Umdrehungszählwerk | DE866563 |
| Mercedes Euklid (Cellatron) | 5/6 S, 13/14 SE, 19 SE/SV, 23/24, 37/38 MS, 43/44 MS | Prop.hebel | Bis 1938 unsichtbares, danach auch sichtbares Summierwerk im Schlitten (ohne Zehnerübertragung); Abspeichern mit Taste S, Rückübertragung in das Hauptzählwerk mit Taste SL. | DE278680 DE691446 DE697151 DE720359 |
| Rheinmetall | KES, KEWS, SASL, SARS | Staffelwalze | Summierwerk im Schlitten, Postenzähler, wahlweise mit Auf- und Abrundungseinrichtung; Modell SARS mit elektrischer Rückübertragung und Speicherlöschung | DE509745 DE571755 |
| Sanders | L'Eclair | Sprossenrad | Erste elektrische Sprossenradmaschine mit Stopdivison, Summierwerk und Postenzähler | DE274744 DE420470 |
| Thales | CES, CER/S, DES, DER/S | Sprossenrad | Stationäres Summierwerk mit Postenzähler, Modelle CER/S und DER/S mit Rückübertragung vom Hauptzählwerk in das Einstellwerk | DE422371 DE541413 DE552133 |
| Walther | SMKZ | Sprossenrad | Wie Modell RMKZ, aber mit Speicherzählwerk |
Parallelwerke. Einige Hersteller von Rechenmaschinen haben ihre Modelle mit einem zweiten Hauptzählwerk ausgestattet. Bei diesen Maschinen kann der Wert aus dem Einstellwerk unmittelbar in beide Resultatwerke eingebracht werden. Das Abspeichern einer Zahl erfolgt hier also nicht durch Übertragen von einem Zählwerk in ein anderes Werk, sondern durch Duplizieren des Werts in zwei Zählwerken. Die zu speichernde Zahl bleibt folglich erhalten und wird nicht - wie beim Summierwerk üblich - aus dem Resultatwerk gelöscht. Die beiden Resultatwerke lassen sich unabhängig voneinander auf Null stellen, und man hat auch die Möglichkeit, eines der beiden Zählwerke abzuschalten. In der Regel können die beiden Hauptzählwerke gleich- oder gegensinnig arbeiten, so daß man beispielsweise eine Zahl zum Wert im ersten addieren und vom Wert im zweiten Resultatwerk subtrahieren kann. Der Aufwand zur Berechnung einer Produktsumme mit Anzeige der Einzelprodukte ist beim Parallel- und Summierwerk etwa vergleichbar. Bei einem Summierwerk muß man jedes Einzelprodukt manuell in den Speicher übertragen, wobei das Hauptzählwerk für die Berechnung des nächsten Produkts automatisch gelöscht wird. Beim Parallelwerk wird die Produktsumme automatisch im zweiten Resultatwerk gebildet, allerdings müssen die Einzelprodukte im ersten Resultatwerk manuell gelöscht werden. Ein Vorteil des Parallelwerks ist jedoch, daß man wahlweise aus dem ersten oder dem zweiten Hauptzählwerk dividieren kann, d.h. sowohl das Endergebnis (Produktsumme) als auch ein Zwischenresultat (Einzelprodukt) läßt sich unmittelbar als Dividend weiterverarbeiten. Andere Vierspeziesmaschinen, wie z.B. die Modelle Brunsviga H und Nova III, wurden mit einem zweiten Umdrehungszählwerk ausgestattet, in dem man unabhängig vom ersten Quotientensummen und -differenzen abspeichern kann. Einen interessanten Entwurf zur Kombination von Parallel- und Summierwerk findet man in der Patentschrift DE375014 von Grimme, Natalis & Co (Brunsviga).
| Hersteller | Modelle | System | Besonderheiten | Patente |
|---|---|---|---|---|
| Archimedes | MZ, GEMRZ | Staffelwalze | Auch Sonderanfertigungen mit hoher Kapazität (MZ 22/24); Division aus beiden Resultatwerken möglich | DE382046 DE760102 |
| Badenia | TE 10 Duplex, TAV 13 Duplex, VARE 17 | Staffelwalze | Division aus beiden Resultatwerken; Beim Modell VARE 17 direkte Addition im Umdrehungszählwerk | |
| Berolina | Duplikator | Sprossenrad | Wie Modell "Berolina Standard", zusätzlich mit zweitem Haupt- und Umdrehungszählwerk | DE392574 |
| Brunsviga | Dupla | Sprossenrad | Direkteinstellung von Werten im ersten Hauptzählwerk, Rückübertragung in das EW aus beiden Resultatwerken | DE463975 |
| Madas | 20 ATG/BTG | Staffelwalze | Zwei Resultat- und Umdrehungszählwerke; Duplex-Werke sind abschaltbar und auch im Vorzeichen schaltbar | |
| Monroe | 66N-213, 88N-213 | Staffelwalze | Automatische Auf- und Abrundung; Division aus beiden Resultatwerken bei Modell 88N-213; Zusätzlich zweites Umdrehungszählwerk | CH296383 US2617594 US2947477 |
Abschaltbares Umdrehungszählwerk. Manche Rechenmaschinen-Modelle bieten die Möglichkeit, das Umdrehungszählwerk als Speicherwerk zu verwenden. Das Umdrehungszählwerk registriert die Anzahl der Umläufe der Antriebsvorrichtung (Sprossenrad, Staffelwalzen usw.) und zeigt je nach Rechenart den Multiplikator, Quotienten oder die Anzahl der Posten bei Addition bzw. Subtraktion an. Folglich wird der Inhalt des Umdrehungszählwerks bei jedem Rechenvorgang verändert. Läßt sich jedoch das Umdrehungszählwerk abschalten, so kann man es zum Speichern und Aufsummieren von Ergebnissen verwenden. Um den Inhalt des Resultatwerks dort additiv bzw. subtraktiv einzubringen, wird bei abgeschaltetem Umdrehungszählwerk das Produkt gebildet und bei eingeschaltetem Umdrehungszählwerk eine Division durch Eins ausgeführt. Bei manchen Rechenmaschinen erfolgt diese "Speicherdivison" automatisch auf Tastendruck. Damit der gespeicherte Wert weiterverarbeitet werden kann, muß eine Rückübertragung aus dem Umdrehungszählwerk in das Einstellwerk möglich sein. Beispielsweise verfügen die Facit CA2-16 und das Nachfolgemodell 1007 über diese Einrichtung. Das Ein- und Abschalten des Umdrehungszählwerks erfolgt hier über die Taste REG II, während ein Wert aus dem Hauptzählwerk mit den Tasten A+ bzw. A- additiv bzw. subtraktiv in das abgeschaltete Umdrehungszählwerk eingebracht wird. Durch Betätigung einer weiteren Taste läßt sich die gespeicherte Produktsumme wieder in das Einstellwerk übertragen.
| Hersteller | Modelle | System | Bemerkungen | UZW abschalten mit, Wert speichern mit |
|---|---|---|---|---|
| Facit | CA2-16, 1007 |
Sprossenrad | Rückübertragung vom Quotientenwerk in das Einstellwerk | Taste REG II, Tasten A+ bzw. A- |
| Friden | ACG, SBT | Staffelwalze | Patente US2656104 und US2687254 | Taste NON ENT, POS/NEG TRANSFER |
| Monroe | CAA, CSA | Staffelwalze | Patentschrift US2620979 | Hebel auf NE ("Non Entry"), Division durch Eins |
| Rheinmetall (Soemtron) |
SARK, 215 | Staffelwalze | Rückübertragung vom Resultatwerk in das Einstellwerk | Hebel, Division durch Eins |
Teilbares Hauptzählwerk. Bei dieser Vorrichtung läßt sich die Zehnerübertragung an einer bestimmten Stelle im Hauptzählwerk unterbrechen, und die zwei Hälften können unabhängig voneinander gelöscht werden. Von den beiden so entstanden Teilwerken kann man eines als Speicherwerk benutzen. Diese Speicherart erfordert eine Rechenmaschine mit relativer großer Kapazität im Hauptzählwerk. Zum Abspeicherung und Weiterverarbeitung der Ergebnisse muß zusätzlich eine Rückübertragungseinrichtung vom (geteilten) Resultatwerk in das Einstellwerk vorhanden sein. Um eine Summe von Produkten und gleichzeitig deren Einzelprodukte anzuzeigen, wird ein Produkt in der rechten Hälfte des Resultatwerks gebildet, in das Einstellwerk zurückgeworfen und nach einer Schlittenverschiebung wieder in die linke Seite des Resultatwerks gebracht (additiv oder subtraktiv). Nach dem Löschen der rechte Seite des Hauptzählwerks kann man das nächste Produkt berechnen. Einen derartigen Speichermechanismus findet man z.B. bei der Handrechenmaschine Brunsviga 20 oder der vollautomatischen Vierspeziesmaschine Friden SBT.
| Hersteller | Modelle | System | Besonderheiten | Patente |
|---|---|---|---|---|
| Badenia | TAVZ 17 | Staffelwalze | Ohne Rückübertragung in das Einstellwerk | |
| Brunsviga | Nova IVa, B 20 | Sprossenrad | Rückübertragung vom Resultatwerk in das Einstellwerk, Splittung des Resultatwerks mit Hebel "partiell" | AT54949 CH58240 |
| Everest | Maxim AR | Sprossenrad | Zehntasten-Einstellwerk ähnlich wie bei Facit, mit Rückübertragungseinrichtung in das Einstellwerk | |
| Friden | STW, ACG, SBT | Staffelwalze | Zählwerksteilung mit Drehknopf am Schlitten, Markierung der Splittstelle, Modell SBT mit Rückübertragung in das Einstellwerk | CH296387 US2722376 |
| Madas | 20 e, 20 LS | Staffelwalze | Resultatwerk von der 8. bis zur 20. Stelle teilbar | |
| Monroe | CAA, CSA | Geteilte Staffelwalze | Hauptzählwerk kann mit Knopf links am Schlitten teilweise oder ganz gesperrt werden |
Zusammenfassung. Rechenmaschinen mit Summier- oder Parallelwerk eigneten sich vor allem zum Abspeichern von Werten mit hoher Stellenzahl, da sie über eine große Speicherkapazität verfügen (mindestens wie das Hauptzählwerk). Diese Maschinen waren jedoch relativ teuer, da sie den Einbau eines zusätzliches Zählwerks erforderten. Modelle mit geteiltem Resultatwerk oder abschaltbaren Quotientenwerk waren dagegen billiger in der Herstellung, da eine bereits vorhandene Konstruktion weitgehend beibehalten werden konnte. Allerdings mußte man hier Einschränkungen in Kauf nehmen: eine geringere Stellenzahl bzw. die fehlende Anzeige des Multiplikators bei der Produktbildung.
3.2 Nichtakkumulative Speicher
Im Gegensatz zu Speicherzählwerken, bei denen ein Wert additiv oder subtraktiv zu einer bereits gespeicherten Zahl hinzugefügt werden kann, besitzen nichtakkumulative Speicherwerke keine Zehnerschaltvorrichtung, d.h. man kann dort nur eine Zahl ablegen. Für die Weiterverarbeitung muß zusätzlich eine Übertragung des gespeicherten Betrages in eines der übrigen Register (Einstellwerk oder Rechenwerke) möglich sein. Solche Wertspeicher lassen sich daher in folgende vier Typen einteilen:
| Speichern aus | Rückwurf in | Speichertyp |
|---|---|---|
| Rechenwerk | Rechenwerk | Multiplikatorspeicher Konstantenwerk |
| Rechenwerk | Einstellwerk | Rückwurfspeicher |
| Einstellwerk | Rechenwerk | Gedächtniswerk |
| Einstellwerk | Einstellwerk |
Multiplikatorspeicher. Einige Vollautomaten verfügen über ein eigenes Multiplikatorwerk, das bei der automatischen Multiplikation auf Null gezählt wird, wobei die Maschine den Multiplikanden im Einstellwerk entsprechend oft zum Hauptzählwerk addiert. Bei manchen dieser Rechenmaschinen besteht die Möglichkeit, den Wert aus dem Hauptzählwerk in das Multiplikatorwerk zu übertragen, so daß er später als Faktor weiterverarbeitet werden kann. Auf diese Weise lassen sich zusammengesetzte Ausdrücke, z.B. Produktsummen, ohne Wiedereintasten der Zwischenergebnisse miteinander multiplizieren. Das Resultat einer solchen Rechenoperation wird im Hauptzählwerk gebildet und kann erneut im Multiplikatorwerk abgespeichert werden. Daher lassen sich auch Mehrfachprodukte a×b×c×… aus beliebigen zusammengesetzten Ausdrücken a, b, c, … in einem Arbeitsgang ermitteln. Die Berechnung von Produktsummen mit Anzeige der Einzelprodukte ist ebenfalls möglich. Hierzu wird das erste Produkt gebildet und im Multiplikatorwerk abgelegt. Die nächsten Produkte berechnet man durch halbautomatische Multiplikation (da das Multiplikatorwerk als Speicher genutzt wird und somit nicht zur Verfügung steht). Eine automatische Multiplikation mit Eins im Einstellwerk addiert schließlich die gespeicherte Zahl aus dem Multiplikatorwerk zum Wert im Resultatwerk. Das Ergebnis legt man als Zwischensumme wieder im Multiplikatorwerk ab, berechnet das nächste Produkt halbautomatisch usw. Solche Multiplikatorspeicher besitzen beispielsweise die Modelle Mercedes Euklid 38 MS, Monroe CSA-10 und Hamann Automatic 500. Bei der Mercedes Euklid läßt sich mit der Taste M die linke Hälfte des Hauptzählwerks in ein unsichtbares Multiplikatorwerk übertragen, das neben dem Umdrehungszählwerk liegt. Bei der Monroe-Maschine, die ein sichtbares Multiplikatorwerk unten am Schlitten besitzt, erfolgt die Übertragung durch Betätigung der CLEAR MULT Taste (siehe Patent US2531208), und beim Hamann-Automaten wird der Wert aus dem Resultatwerk durch Betätigung der Taste X in das Multi-Werk gebracht.
Rückwurfspeicher. Bei der Handkurbelmaschine Madas 10 R oder der halbautomatischen Rechenmaschine KEL IIc RS von Rheinmetall kann der Inhalt des Hauptzählwerks in einem Zwischenspeicher abgelegt werden, der gleichzeitig auch zur Aufnahme des Wertes bei der Rückübertragung verwendet wird (siehe das Patent CH218923 bzw. DE889843 von H.W. Egli). Bei der Madas 10 R ist hierzu eine "Löffeltaste" auf der rechten Seite vorhanden, mit der ein Wert aus dem Hauptzählwerk in das sichtbare Speicherwerk unterhalb der Tastatur übertragen wird. Der Speicherinhalt kann später mit einem Hebel auf der linken Seite in das Einstellwerk zurückgeholt werden und steht so für eine Weiterverarbeitung zur Verfügung. Ähnlich arbeitet das Rheinmetall-Modell KEL IIc RS: Bei der normalen Rückübertragung werden zugleich mit dem Löschen des Hauptzählwerks eine Reihe von Hilfsstaffelwalzen gedreht, die den Einstellweg für die einzelnen Tastenreihen festlegen. Durch Betätigung einer speziellen Speichertaste S können die Hilfsstaffelwalzen aus dem Einflußbereich der Tastenreihen geschwenkt werden, so daß der Wert aus dem Hauptzählwerk dort gespeichert bleibt. Erst durch nochmaliges Drücken der Rückübertragungstaste wird der gespeicherte Wert in das Einstellwerk gebracht und außerdem noch zum aktuellen Wert im Hauptzählwerk addiert. Eine bemerkenswerte Weiterentwicklung dieser Speichertechnik findet man in den Patentschriften US2909320 und US3045907 von Arthur J. Malavazos, einem Mitarbeiter der Firma Friden. Die geplante Maschine hat ein sichtbares Speicherwerk unterhalb der Volltastatur, in das man ein Ergebnis aus dem Hauptzählwerk oder dem Quotientenwerk ablegen kann. Der Wert wird auch hier in Stufenwalzen gespeichert und kann jederzeit in das Einstellwerk eingebracht werden. Diese Konstruktion wurde jedoch nie in einer Rechenmaschine umgesetzt stattdessen hat man das Modell Friden SBT mit vereinfachtem Rückübertragungsmechanismus gebaut (siehe z.B. das Patent US3249301).
Konstantenwerk. So wird von einigen Herstellern eine Speichervorrichtung in druckenden Vierspeziesmaschinen bezeichnet, die ein Rechenergebnis aus dem Haupt- oder Umdrehungszählwerk aufnimmt, wobei der dort abgelegte Wert zu einem beliebigen Zeitpunkt wieder in das ursprüngliche Zählwerk übertragen werden kann (siehe Abschnitt 3.3). Bei nichtdruckenden Vierspeziesmaschinen ist diese Einrichtung eher selten. Einen derartigen Konstantenspeicher findet man jedoch bei den Pendelradmaschinen Olympia RA 16 und RA 20. Das Konstantenwerk liegt hier unsichtbar hinter dem Umdrehungszählwerk und wird mittels eines Schalthebels rechts auf dem Schlitten aktiviert. Ist es eingeschaltet, so kann man eine Zahl aus dem Umdrehungszählwerk durch Nullstellen desselben in das Konstantenwerk übertragen, und bei der Multiplikation läuft der Faktor, der aus dem Umdrehungszählwerk abgearbeitet wird, automatisch in den Konstantenspeicher ein. Mit Hilfe eines weiteren Hebels ("Einzugshebel") wird die gespeicherte Zahl aus dem Konstantenwerk wieder im Umdrehungszählwerk eingestellt. Bei ausgeschaltetem Konstantenwerk kann man das Umdrehungszählwerk für weitere Rechenoperationen verwenden, ohne daß der gespeicherte Wert verändert wird.
Gedächtniswerk. In dieser Speichervorrichtung läßt sich ein Wert aus dem Einstellwerk ablegen, so daß er später wie eine eingetastete Zahl weiterverarbeitet werden kann. Ein Beispiel hierfür ist das Multiplikatorspeicherwerk der Sprossenradmaschine FACIT ESA (vgl. Patent DE922553), das gleichzeitig mit dem Eintasten den Wert aus dem Einstellwerk übernimmt. Die gespeicherte Zahl oder ein Vielfaches davon läßt sich jederzeit zum Inhalt des Resultatwerks hinzufügen, indem man mit Eins oder einem entsprechenden Faktor multipliziert. Der Multiplikator bleibt hierbei erhalten, da er nicht durch Löschen, sondern durch Abtasten an den Multiplikationsmechanismus weitergegeben wird. Bei dieser Konstruktion besteht allerdings nicht die Möglichkeit, einen Wert aus dem Haupt- oder Umdrehungszählwerk im Multiplikatorspeicher abzulegen. Ein Gedächtniswerk besitzt auch das Modell Badenia VA 17. Dort kann mit Hilfe eines Schiebers auf der linken Seite der Wert aus dem Einstellwerk zwischengespeichert und später wieder in das Einstellwerk zurückgeholt werden. Mit dieser Einrichtung läßt sich demnach eine Zahl als konstanter Summand, Subtrahend, Multiplikand oder Divisor bereithalten. Verfügt die Maschine neben einem solchen Gedächtniswerk auch noch über eine Rückübertragungseinrichtung vom Hauptzählwerk in das Einstellwerk, wie z.B. das Modell VARE 17 von Badenia, so ergeben sich fast unbegrenzte Speichermöglichkeiten: Eingetastete Werte oder Rechenergebnisse können im Gedächtniswerk zwischengelagert werden, und die gespeicherte Zahl läßt sich dann über das Einstellwerk als Operand in allen vier Grundrechenarten verarbeiten. Eine weitere Besonderheit der Badenia VARE 17 ist die elektromechanische Rückübertragungseinrichtung, mit der sowohl der Inhalt des Hauptzählwerks als auch auch der Wert aus dem Umdrehungszählwerk direkt in das Einstellwerk gebracht werden kann, wobei die zu übertragende Zahl wahlweise auch im ursprünglichen Zählwerk erhalten bleibt.
3.3 Druckende Vierspeziesmaschinen
Schnellaufende Vierspeziesmaschinen, die mit einem Druckwerk ausgestattet sind, arbeiten in der Regel mit oszillierenden Zahnstangen, um Zahlen zwischen den einzelnen Registern (Einstellwerk, Rechenwerke, Druckwerk und Speicherwerk) auszutauschen. Für die Übertragung des Werts von einem Zählwerk in das Speicherwerk müssen zunächst die Zahnräder der beteiligten Register mit den Zahnstangen in Eingriff gebracht werden. Beim Nullstellen des Rechenwerks verschieben sich die einzelnen Zahnstangen um einen Betrag, der den Ziffern der zu übertragenden Zahl entspricht. Diese Bewegung wird an die Zahnräder des Speicherwerks weitergegeben, das anschließend von den Zahnstangen entkuppelt wird und den eingestellten Wert behält. Soll der Speicherinhalt wieder in eines der übrigen Zählwerke zurückgebracht werden, dann läuft der Vorgang in umgekehrter Weise ab: Der Speicher wird mit den Rechenzahnstangen gekoppelt und gelöscht, wodurch der gespeicherte Wert an das mit den Zahnstangen verbundene Rechenwerk übertragen wird. Da die Zahnstangen eine oszillierende Bewegung ausführen und für die Werteübertragung nur eine Richtung, etwa die Vorwärtsbewegung, erforderlich ist, kann der gelöschte Speicherinhalt wiederhergestellt werden, indem das Speicherwerk auch bei der Rückwärtsbewegung mit den Zahnstangen in Eingriff bleibt. Ein derartiger Mechanismus erlaubt sowohl das Verschieben als auch das Kopieren des gespeicherten Wertes von einem Zählwerk in ein anderes, und daher kann man die Abfühlzahnstangen der "Printing Calculators" als mechanische Vorläufer des Datenbusses im Computer ansehen. Bei einer solchen Konstruktion können Speicherwerke in beliebiger Anzahl vorhanden sein, und sie benötigen keinen Zehnerübertragungsmechanismus, da die Werteverarbeitung in einem zentralen Rechenwerk erfolgt. So arbeitet beispielsweise das "Druckende Rechensystem" Diehl Decima S mit einer Sprossenrad-Schnellrecheneinheit zum Multiplizieren und Dividieren, wobei die Ergebnisse automatisch in ein akkumulatives Speicherwerk übertragen werden. Dessen Inhalt läßt sich durch Betätigung einer Taste für Zwischen- oder Endsumme auf einem Papierstreifen ausdrucken. Ein zusätzlicher Konstantenspeicher (ohne Zehnerübertragung) bietet die Möglichkeit, einen Wert beliebig lange für jede Rechenart festzuhalten, und auch die zuletzt gedruckte Zahl kann aus dem Druckspeicher wieder zur Weiterverarbeitung abgerufen werden. Bei der Diehl Transmatic S besteht darüber hinaus die Möglichkeit, Produkte und Quotienten wahlweise in einem von zwei Speicherwerken abzulegen. Für ausführlichere Informationen zum Speichermechanismus der druckenden Diehl-Rechenmaschinen sei auf die Patentschriften DE1449490 (Hilfswerksteuereinrichtung; Becker/Eggebrecht/Steinmeyer) und DE1424874 (Einrichtung zum Aufrunden eines Produkts; Metschnabel/Burkhardt) verwiesen. Weitere Vierspeziesmaschinen mit Druckwerk und zum Teil mehreren Speichereinrichtungen sind etwa die Modelle Precisa 166 (vgl. Patent DE1033939), Olivetti Logos 27 (Patent DE1474677) und Hamann 600 (Patent CH486067, siehe auch den Artikel von Anthes [9]).
3.4 Kombinierte Speichervorrichtungen
Die Speichermechanismen wurden bis zum Ende des Zeitalters mechanischer Vierspezies-Rechenmaschinen (Anfang der 1970er Jahre) fortlaufend ausgebaut und kombiniert. Eine vollständige Auflistung aller Modelle und ihrer Speichermöglichkeiten würde den Rahmen dieser Übersicht sprengen. Daher sei als Beispiel für eine nicht-druckende Vierspeziesmaschine, die verschiedene Speichervorrichtungen vereint, das Modell Monroe IQ-213 besonders erwähnt. Diese Staffelwalzenmaschine besitzt ein Speicherwerk, dessen Inhalt in das Einstellwerk zurückgebracht oder als konstanter Multiplikator verwendet werden kann. Mit der Taste ENTER MEMORY legt man einen Wert im Speicher ab, und die gespeicherte Zahl wird anschließend in einem Kontrollwerk oberhalb der Tastatur angezeigt. Die Taste RECALL MEMORY bewirkt eine Rückübertragung des Speicherinhalts in das Einstellwerk, während MEMORY MULT einen Wert aus dem Einstellwerk mit der gespeicherten Zahl multipliziert. Darüber hinaus verfügt dieses Modell über ein gesplittetes Hauptzählwerk, zwei unabhängige Umdrehungszählwerke sowie eine Vorrichtung zur Rückübertragung vom Resultatwerk in das Einstellwerk. Kombinierte Speichervorrichtungen findet man z.B. auch beim Modell Friden SBT (geteiltes Hauptzählwerk und abschaltbares Umdrehungszählwerk) oder in den Proportionalhebelmaschinen Mercedes Euklid (Summierwerk und Multiplikatorspeicher).
4 Abschließende Bemerkungen
Die hier vorgestellten Grundprinzipien sollen einen Eindruck von der Vielfalt unterschiedlicher Speichervorrichtungen vermitteln und zugleich zeigen, welche Möglichkeiten bereits in der mechanischen Rechentechnik vorhanden waren. Die aufgelisteten Vierspeziesmaschinen und Patentschriften lassen auch einen gewissen Trend erkennen: Anfangs wurden Speicherverfahren fast ausschließlich in Europa (Deutschland, Schweiz) entworfen. Dies änderte sich allerdings in den 1950er Jahren. Die wenigen, aber großen Rechenmaschinen-Hersteller aus den USA trugen viele neue Ideen zum Auf- und Ausbau von Speichervorrichtungen bei, und dort hat man auch einige der komplexesten und beeindruckendsten Rechenmaschinen-Modelle produziert, wie z.B. den "Speicherautomaten" Monroe 88N-213 oder das Monroe-Modell IQ-213. Es wäre sicherlich interessant zu erfahren, wie sich die Entwicklung der mechanischen Speichertechnik ohne den Einfluß der Elektronik fortgesetzt hätte. Vielleicht gibt es aber auch noch Speichervorrichtungen, die hier nicht erfaßt wurden. Ich würde mich über weitere Informationen diesbezüglich sehr freuen. An dieser Stelle möchte ich mich auch bei Mark Glusker und Heinz Metzen für die Bereitstellung von Bildern und Unterlagen sowie für zahlreiche Anregungen ganz herzlich bedanken.
5 Literatur
[1] Cornelius Veithen: "Über die Verwendung der Rechenmaschine bei der Bahnbestimmung von Planeten", Dissertation, Göttingen 1912.
[2] Walter Meyer zur Capellen: "Mathematische Instrumente", dritte (ergänzte) Auflage, Akademische Verlagsgesellschaft Geest & Portig, Lepzig 1949.
[3] Friedrich A. Willers: "Mathematische Maschinen und Instrumente", 3. Auflage, Akademie-Verlag, Berlin 1951.
[4] A. Hennemann: "Die technische Entwicklung der Rechenmaschine", Büromarkt-Bibliothek Band 8, Verlag Peter Basten, Aachen 1953.
[5] Otto Priebe: "Rechenmaschinen im Büro, Teil 1: Was muß man von Vierspeziesmaschinen wissen?", Robert Göller Verlag, Baden Baden 1955. Speziell im Abschnitt 3,3 g), Seite 29 34, werden Speichervorrichtungen behandelt.
[6] Neuzeitliche Bürotechnik / Büromaschinenlexikon, verschiedene Jahrgänge ab 1957, Göller-Verlag, Baden-Baden.
[7] Francis J. Murray: "Mathematical Machines, Volume 1: Digital Computers", Columbia University Press, New York 1961.
[8] Erhard Anthes: "Die Kuhrt-Rechenmaschine", in: Büro-Wirtschaft, Mai 1988.
[9] Erhard Anthes: "Die Mercedes Euklid 1910-1970" und "Die letzte Hamann-Rechenmaschine: Modell 600", Beiträge zur Geschichte der mechanischen Rechenmaschine, Grünes Heft Nr. 22, Didaktisches Zentrum der Pädagogischen Hochschule Ludwigsburg, 1998.
[10] Martin Reese: "Neue Blicke auf alte Maschinen - Zur Geschichte mechanischer Rechenmaschinen", Verlag Dr. Kovac, Hamburg 2002.
[11] Heinz Metzen: "Brunsviga 20 ein 'Dauerläufer' von 1934 bis 1964", HBw-Aktuell 04/2004.
[12] Erhard Anthes: Mechanische Rechenmaschinen für wissenschaftliche Berechnungen (Autorentext im Rechnerlexikon).
6 Weblinks
Weitere Bilder und Daten zu den aufgelisteten Rechenmaschinen-Modellen findet man hier im Rechnerlexikon sowie auf folgenden Internetseiten:
[13] Mark Glusker:  "Electromechanical calculating machines from the 1960's"
"Electromechanical calculating machines from the 1960's"
[14] John Wolff's Web Museum,  "Calculating Machines"
"Calculating Machines"
[15] Michael Landwehr,  Rechenmaschinensammlung
Rechenmaschinensammlung
7 Copyright
Alle Rechte beim Verfasser
Erstellt von: Harald Schmid 06:47, 24. Mär 2006 (GMT)
Anschrift des Verfassers:
- Harald Schmid
- Mosacherweg 39
- 92224 Amberg
- E-Mail: harald.schmid@online.de
Diese Seite ist geschützt. Sie darf nur vom Autor oder einer beauftragten Person verändert werden.
Falls Sie mit dem Inhalt nicht einverstanden sind, machen Sie bitte einen Eintrag bei der Diskussion und schicken dem Autor eine Mail.
- Patent:AT61296B 01.04.1911 Pöthig, Reinhold :
Thomas sche Rechenmaschine mit zwei hintereinander liegenden Zählwerken
![[Hauptseite]](/upload/wiki.png)
 Hauptseite
Hauptseite